WAP (Python) to check if a number is an Armstrong Number or not

Hey all, today we are going to check if a number is an Armstrong number or not. So gear up as we are going to do this problem in the best way possible!!! 

As always, if you want the final code for this program, you could find it at the end of this article. But rather, it would be good if you stay with us the whole journey as we are going to go through each and every step you need to follow to become the best coder. Excited? Let's start!!!

Also read: WAP (Python) to print the nth term of the Fibonacci Series

What is an Armstrong Number?

In simple language, if a number of order (number of digits) 'n' is equal to the sum of the nth power of its digits, then its called an Armstrong Number. Understood? Most probably no! Let's take a simple example:

The number 153 has 3 digits, hence its order is 3. Also, the value of 1³ + 5³ + 3³ is also equal to 153. So this is an Armstrong number. Other example of Armstrong Numbers are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407..... and many more.

Hence if we want to write the general formula for Armstrong numbers:

xyz...(n digits) = xⁿ + yⁿ + zⁿ..... 

I hope you are now able to understand what an Armstrong Number really is. Now let's start with the overview!!!

Overview:

In this program, we are asked to check whether the number entered by the user is an Armstrong Number or not. The input required would be the number itself and then we would be using while loops to do the rest of the program. 

*As I have already told you the basics, you could try doing the program on your own. See if the answer matches!*

Understanding what we need to do:

Here I will tell you step by step what you need to do.

Step 1: Asking the user for the input:

The first and the easiest step would be to ask the user for the input. I have named the variable 'n'. And while asking the for the input, we will make sure we type-cast it into an integer, as we have to perform calculations with it.

Here's the code for this step:

Step 2: Checking if the number is an Armstrong Number or not:

Now from the input we have got, we need to find the number of digits of the number. I have named the variable as 'order'. To find its length, we need to use the 'len' function and to use it, we need to typecast it into a string, which you can see I have done in the first line itself.

Next we want a variable to store the sum of the nth power of the digits. Let's call the variable, 'sum', it is initialised to be equal to 0. We have also declared another variable 'copy_n' whose role would be explained later in this article.

Now in the looping part: 

As we have now got the order of the number, our next task is to find each and every digit, so that we can sum them up. To do this, we make use of the concept of remainders. If we divide a number by 10, then the remainder would be the last digit of the number. I have taken it to be equal to the variable 'digit'.

For example: In the number 153:

153%10 = 3. This gives the the last digit of the number.

Next we need to do the most important part, finding the sum of these digits. Here, the sum should be equal to the value of [digit**order], where ** means 'to the power'. And as with every loop, we need to add the previous sum to the new sum, we have used to operator '+=' instead of just '='.

Now, to exclude the last digit from number, so that the next loop can run, we need to use the 'Floor Function'. It is just another name of the 'Greatest Integer Function'. You can read about it's usage in any math's forum, but the main use of it in this program is that, in a division, it only gives us the integral part of the quotient. The operator used for it is '//'.

For example: In the number 153:

153/10 = 15.3 but 153//10 = 15

Hence you can see that it is important for the next loop to run. I have saved its value in the variable 'n' itself. Now, this loop will run until n>0.

Also read: WAP (Python) to find the factorial of a given number

After the loop ends, we need to make if-else statement to check whether its equal to the original number or not. * But you may have noticed that the value of n (initial number) has been changing continuously in the loop itself, hence we can't refer to it now. So here comes the use of making a copy of n, whose value won't get altered. I named the variable as 'copy_n', which I declared in the starting itself!*

If the value of sum equals the value of 'copy_n', then the number would be an Armstrong Number, but if it isn't, then it won't be an Armstrong Number.

*Note: In the program, while using the print statement, we wrote 'f' before the ", so that we could show the user the initial number along with other words. Its just a better way of printing numbers along with strings.*

Here's the code for this step:

So now, we have found the best way to check if a number is an Armstrong Number or not!

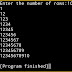
Here's the full code:

And here ends our amazing journey where we found the best way to check if a number is an Armstrong Number or not. I really hope you liked this article, and if you did, then don't forget to share it so that everyone struggling with coding can get help!!!

Your next challenge is:

WAP to check if a string/number is a palindrome or not.

In the next article, we would be finding the answer to this question, so stay tuned. Till then, keep coding!!!

Here's the article for the above question: WAP (Python) to check if a string/number is a palindrome or not

Also, please consider subscribing to our newsletter as we do these coding sessions regularly.

Again, thanks for reading!!!